The Zmynx system of jazz scale notation
Revised June 2008
This is the system I use for writing the scales used in jazz improvisation.
Playing a jazz song, number or tune requires the improviser to move through a progression of different musical scales, improvising on each one in turn. While the song as a whole is considered to be in a particular key (the key in which the melody or head begins and ends), we need to specify a number of key changes within the song, relating them to the original key. Each key change represents a change of scale.
Every scale is anchored to its own root note, key note or tonic note. We shall call this the scale tonic. We shall call the original key of the song as a whole the home tonic, and the corresponding scale the home scale.
What we are after is to be able to write down a sequence of scale tonics, with additional information specifying what kind of scale (major, minor, etc.) is to be played on each one, and for how many bars.
There are two ways of writing a scale tonic: either we state the specific note itself (C, D, E, ...), or we state its position relative to the home tonic (1, 2, 3, ...). Thus if we take a song in the key of C, we may for example play some bars in a scale whose tonic is the fifth note of the home scale. If we say that this note is G, then it and its accompanying scale can be found very quickly on one’s instrument, but this will only remain true so long as we play the song in C. But if we call the fifth note “5”, then its identity as 5 will remain true if we decide to play the song, not in C, but in F, or Bb, or any other key.
But won’t it take longer to work out what the 5th note is in any scale? I don’t think so. Suppose you’re playing a tune by ear – or singing it. You hear the next note in your mind, and you automatically identify the interval you want and jump to that note. In other words, thinking in relative terms is actually more natural – it’s only its unfamiliarity that makes one want to cling to the intellectual security of a specific named note.
This is easy to see once one is familiar with the 2-5-1 chord progression. Any competent musician will have practised this in all keys, and will know immediately how to play it in any given situation. Specifying which actual note the “2” begins on is superfluous: it’s just the 2nd of whatever key or home scale you’re in.
So an efficient system of notation will obviously be able to represent scales both ways – specific or relative – with equal ease. But this is not true of the existing musical notation.
If, for example, C7 represents a scale whose tonic is C and whose 7th note is a minor 7th, then why do we not denote a scale whose tonic is the minor 7th of the home scale and which itself has a minor 7th as “77”? Or if Cm is C minor, i.e. with a minor third, why do we not write the scale of Eb with a minor 7th as “m7”?
Certainly, there does exist a system based on roman numerals I-VII, but these are clumsy to use, because they are not designed to take account of the accidentals (the five notes not on the basic major scale), and because of the inherent clumsiness of roman numerals.
Enter the Zmynx system.
In the basic Zmynx system, we write the relative chromatic scale in the following way:
| 1 n_2 m_3 4 x_5 y_6 z_7 |
1 is the tonic or key note, 2 is the major 2nd, 3 the major 3rd, and so forth, covering all seven notes of the standard (ionian) major scale. The five letters are regarded as the minor or flat variation of the note above, thus n is a minor 2nd, m a minor 3rd, x a diminished 5th, and so on. (The underscore in the diagram is to remind us that, say, m is connected to 3, i.e. is a flat 3rd, and is not normally used to represent a sharp 2nd.)
When writing scales, we use a specific note such as C to represent the standard (ionian) major scale with that note as scale tonic: C D E F G A B C. This matches standard practice.
We use the letters n m x y z to represent variations on that major scale. Cz has a Bb instead of a B natural, Cmz has in addition an Eb instead of an E natural, and so on.
Unlike standard practice, we use this system to specify the scale exactly, including all variations from the major scale.
Again unlike standard practice, we may use the letters and numbers themselves as scale tonics. If a song is in the home key of C, then 1 will represent the major scale of C, 5 will represent the major scale of G, 3z will be the major scale of E with a minor, flat or dominant seventh note (E F# G# A B C# D E), mmz will be the dorian minor scale of Eb, and so on.
The first character always represents the scale tonic, either specific or relative. Any following characters represent variations on the major scale constructed on that scale tonic. Thus the two letters m in “mmz” mean different notes: the first says: “take as your scale tonic the minor 3rd of the home key of the song”, while the second says: “your new scale for improvising has a minor, not a major, 3rd” – in other words the first m counts a minor 3rd up from the home tonic, the second m counts another minor 3rd up from the first m.
(It would be possible to capitalise a letter being used as a scale tonic, but we don’t do this because a capital Z could easily be confused with the number 2.)
zz is another common scale, it means: whatever home key you’re in, go to the scale whose tonic is the minor 7th, and play on that scale tonic in a scale which itself has a minor 7th in it. If the song is in C, we will therefore play at this point in Bbz (traditional notation: Bb7 or Bb7); if we decide instead to play the song in say Ab, the same zz will put us in the scale of Gbz (Gb7).
Sometimes we want to specify a scale without relating it to any particular tonic at all: in this case, we use the letter K as a dummy key note. Thus K by itself represents the ionian major scale in any key, Kmz the dorian minor in any key, and so on.
We can now list the scales at our disposal, and compare the Zmynx notation with the traditional ways of writing them (related to the key of C, as standard notation does not have the concept of a dummy key note). We begin with six of the seven modal scales, which neatly show how we can generate one scale from another by adding one flat at a time:
| K | major scale (ionian mode) | C, CΔ |
| Kz | dominant 7th scale (mixolydian mode) | C7, C7 |
| Kmz | minor scale (dorian mode) | C-, Cm, Cmin, C-7, Cm7, Cmin7 |
| Kmyz | descending melodic minor (aeolian mode) | C-b6 |
| Knmyz | phrygian mode | C-b9b6 |
| Knmxyz | half-diminished scale (locrian mode) | Cφ, Cm7(b5) |
Beyond the modal system, we can add the following scales:
| Km | ascending melodic minor scale | C-Δ, CmΔ, CminΔ, Cm6 |
| Kmy | harmonic minor scale | C-Δ, CmΔ, CminΔ, CminΔb6 |
| Kmxyz | half-diminished scale with major 2nd | Cφ#2, Cφ+2, Cφ9 |
| Kyz | Hindu scale | – |
| Knyz | Spanish or Jewish scale | – |
Note that the Zmynx system allows us to specify exactly which of several minor scales we want. The existing system is imprecise and ad hoc. For example, C- represents Cmz: the minus sign lowers both the 3rd and the 7th. If we now want a scale with a minor 3rd only, we have to introduce a symbol to cancel part of the action of the minus sign, thus C-Δ. There is no system for showing whether a minor scale is harmonic, melodic ascending or melodic descending. In the Zmynx system, we specify in the most economical fashion which notes belong to the scale.
This is useful in a song like “What Is This Thing Called Love?”, whose fifth and sixth bars need 5yz (not 5z, as one might expect – the y note of the 5th scale is m of the home scale, and thus produces a minor effect distinctive of this song).
All minor scales have in common a minor 3rd, and we can use Km to specify economically that a song as a whole is in a minor key, since the 6th and 7th are unstable and often vary between major and minor within a melody.
One further point is that we are writing the letters n m x y z in order, i.e. ascending pitch going up the scale. This enables us to distinguish between say a flat 2nd and a flat 9th, so long as there are other flat notes present, e.g. Knmz would have a flat 2nd, whereas Kmzn a flat 9th. The flat 9th is sometimes specified in a song, and, though it is really an instruction for playing a chord rather than a improvisation scale, it is still useful to prompt a soloist to try playing that note flat in the higher register.
Given these scales, we need to know how long to play on a particular one. To do this we can either use the traditional format of drawing a table (as in the example that follows), or we can put the number of bars in brackets after the scale symbol, using if necessary (h) for a half bar and so on.
Take a specific example: “Out Of Nowhere”. A player on keyboard, guitar or bass will need all the chord changes, but a single-note soloist on sax, trumpet, trombone, flute, violin, melodica etc. can perform better with a simplified version of the song’s harmonic structure, and this is what we present here.
In traditional notation, the chord changes or scale progression of “Out Of Nowhere”, played in its usual home key of G, go (each box in the table lasting two bars):
| G | Eb | G | Bm7 |
| Am7 | Am7 | Gm7 | D7 |
| G | Eb | G | Bm7 |
| Am7 | Am7 | D7 | G |
Using our specific Zmynx notation, this changes only slightly:
| G | Eb | G | Bmz |
| Amz | Amz | Gmz | Dz |
| G | Eb | G | Bmz |
| Amz | Amz | Dz | G |
But this can now be rewritten in relative form, applicable whatever key the song is played in:
| 1 | y | 1 | 3mz |
| 2mz | 2mz | 1mz | 5z |
| 1 | y | 1 | 3mz |
| 2mz | 2mz | 5z | 1 |
Note how the final 8-bar section is written in such a way that the 2-5-1 progression is explicit and obvious.
On my crib sheet, I write it in more compact form, using [A], [B] etc. for each 8-bar section of a song:
| Out Of Nowhere [ABAC] |
| [A] = 1(2) y(2) 1(2) 3mz(2) [B] = 2mz(4) 1mz(2) 5z(2) [A] (repeat) [C] = 2mz(4) 5z(2) 1(2) |
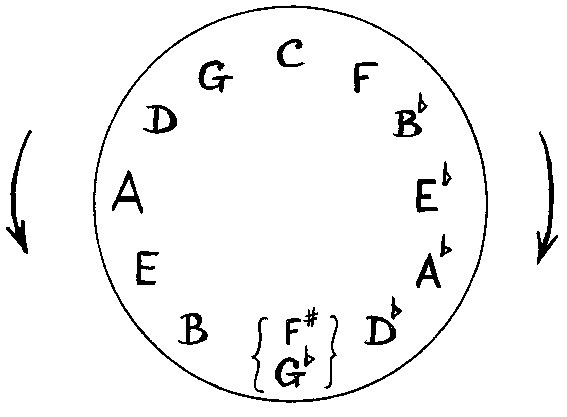
Progressions around the cycle of 5ths are common in jazz. The reader should already be thoroughly familiar with the clock-face which shows how keys have been related to each other in Western music since the time of Bach’s “Well-Tempered Clavier”:
up
 down
down |
I think of moving from key to key in an anticlockwise direction as moving up the cycle of 5ths, while going in a clockwise direction is moving down – partly because G is a 5th above C while F is a 5th below it, but even more because of the musical equivalent of a law of gravity tending to resolve a key by settling on the key below it.
So in the middle 8 of “I Got Rhythm”, for example, you jump up four keys (the tune is normally played in Bb, so you switch to Dz for two bars) and then step down one key at a time until you return to the home key (i.e. from Dz to G, then to Cz, then to Fz, ready to return to Bb in the final 8 bars of the song).
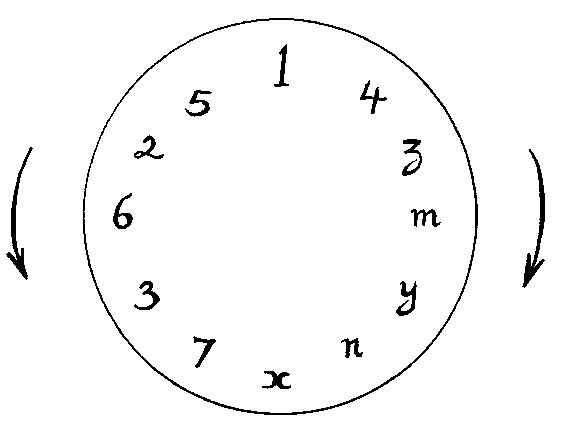
The Zmynx system can be represented by a similar clock-face:
up
 down
down |
This relativises the cycle of 5ths shown before. Imagine the two clock-faces superimposed. The Zmynx face is allowed to rotate, and therefore shows the relationship of any note on the scale to any key. If it is rotated so that 1 coincides with, say, Eb, then you can immediately read off, say, that the 6th of the scale is C, the minor 3rd (m) is F# or Gb, and so on. Of course this merely represents on a diagram all the information that a competent musician will know immediately and automatically once he or she has mastered scales on all twelve possible key notes.
But the diagram also shows that, starting with a scale whose key note is 4 (relative to whatever the home tonic may be), stepping down the cycle of 5ths key by key takes us successively through keys whose tonics are z, m, y, n and x – hence the name for the system as a whole is a mnemonic for the relationship of some of the keys to each other.
Historical note – my motivation for inventing the Zmynx system was to have an efficient system of notation independent of the key. Thinking of chord changes or scale progressions in a relative sense (talking of the 3rd, 5th, etc. of the scale rather than E, G, etc., or B, D, etc., or F#, A, etc., ...) helps you to understand the music better. It also helps you to transpose to another key.
This is particularly useful if you possess transposing instruments – at the time of writing, I own saxophones in Eb, Bb and C – and, while we’re on the subject, an alto flute is pitched in G, while a cor anglais or mezzo-soprano sax (extremely rare!) is in F, and an oboe d’amore in A.
It’s also useful if you’re working out the chords for, say, “Corcovado”, which is printed in C, but on the CD Stan Getz and Astrud Gilberto perform it in Bb. Of course, whenever you’re performing with a singer, he or (more likely) she will very often want to sing in a different key from the one given in the printed music for that song, because of the way different people’s voices vary. And in any case, playing the same tune in different keys is an important part of a musician’s practice routine.
So a key-independent musical notation is a must.
My first thought was to represent the major scale with the numbers 1-7 and the five accidentals with the letters v-z. The number 7 resembles part of a letter z, so the step from writing say C7 to Cz is an easy one. We then have all the numbers representing naturals and all the letters representing flats: neat and logical.
As it stands, this system would represent a minor 3rd with the letter w. Why not invert the w, to get an m? Then the characteristic note of the minor scale (the 6th and 7th may or may not be flattened) would be exactly the same as one of the standard ways of writing a minor scale. At the same time, why not invert the v too, to get an n? Then the n, with two legs, for a flat 2nd, would match the m, with three. At the same time, using m and n gives us a (more or less) pronounceable word as a mnemonic for the relationship of the five accidentals on the cycle of 5ths. So Zmynx it became.
More complex scales – what I want to do now is to introduce one refinement to the basic system, to adapt it to show sharp notes.
We are using x for a flattened or diminished 5th. Suppose instead we want to show an augmented 4th. This is of course exactly the same note as the diminished 5th (or it is on the well-tempered clavier; string players historically drew a distinction between a sharp note and the flat of the note above it – I don’t know whether they still do). I shall place the x in superscript position to indicate that, rather than its normal use as the flat of the note above, I now want it to show the sharp of the note below it.
So Kx represents the lydian mode. For example, in the key of C, 1x will be the scale: C D E F# G A B C. The theme tune to “The Simpsons” is played on a lydian scale.
This allows us to write some jazz scales which go beyond the basic major and minor variations.
From time to time we want a scale with an augmented 5th, and this can now be written efficiently as Ky. For example, the song “Close Your Eyes” needs a Bb yzn (writing the n at the end gives us a flat 9th).
The diminished scale is Kmxy, which is quite easy to understand: it tells you that you want a minor 3rd, and both augmented and diminished 5ths instead of the perfect 5th. All the other notes are the same as in the major scale.
The altered scale is supposedly one in which all notes except the tonic are flat. This can also be described as the 7th mode of the ascending melodic minor scale, and it falls outside the sequence of well-behaved scales. Actually, it is easier to understand and play as a normal major scale in which the only change is that the tonic is sharp: Kn.
The whole tone scale can be written Kxxyz – i.e. it has both an augmented 4th and a diminished 5th, and since these are the same note the scale obviously only has six notes.
What about the blues and bebop scales? These are listed as variant scales in the Aebersold books. But they are not scales so much as styles. The blues scale is basically a dorian minor (Kmz) with specific colour provided by the use of the “blue note” x, additional to the 4th and 5th, not replacing them. Again, the bebop scales may have both a minor and major 3rd, or 6th, or 7th.
These variants do not represent scale changes in the sense that a 2-5-1 progression does, but rather embellishments to scales such as the dorian minor. They are stylistic variants rather than harmonic ones, and therefore do not form part of the structure of a song, and do not need a special notation or scale symbol.
Modality of scales – now here’s an interesting bit of music theory for us music theory fans. If you take the 4th note of the standard major scale and jump to the note a perfect 5th above it, then to the note a 5th above that, and so on, you can construct a continuous sequence of 5th intervals, broken only at the two ends of the sequence, which do not join up because the scale includes only 7 notes out of the 12 possible ones. Thus for example in the scale of Bb you have the sequence of notes:
Eb Bb F C G D A
This is surely related to the fundamental importance of this scale in music. The 5th interval is the simplest relationship between musical notes because of the physics of sound production, and the standard major scale contains the maximum number of 5ths given a seven-note scale.
A scale can be constructed upon each note in the home scale, using only the notes in that home scale. Again using the key of Bb as an example, these scales are as follows:
Eb x Bb Fz Cmz Gmyz Dnmyz Anmxyz
These scales thus form a sequence in which each scale has one more flat note relative to one neighbour, and one less relative to the other. In other words, the scales are all modes of each other.
The melodic (ascending) minor (Km) and harmonic minor (Kmy) scales are not well-behaved in this way. They do not form a continuous sequence of perfect 5ths – that sequence is broken before all seven notes of the scale have been accounted for. But where they do form a continuous sequence of 5ths, again the scales built on those notes themselves form a continuous sequence in which one flat is gained or lost as you pass from each one to its neighbour.
These scales are also included within the notation of the Zmynx system, though they are not often used.
We have talked about chord changes and scale progressions. When is a chord a scale, and when is it not?
The two are closely linked. A chord can be regarded as some of the notes of a scale, spaced in thirds (usually), and played simultaneously or in a pattern such as an arpeggio. Thus the chord of C major might be played as the ascending series of notes C, E, G, B. If we continue the series of notes with D, F, A, C (the 9th, 11th, 13th and 15th), we will cover every note of the scale. At the same time, the corresponding melody will also be played using the scale composed of these same notes, and accidentals (the notes not part of the chord or scale) will be employed sparingly, to create extra interest and colour.
So if we write, say, Dmz – or, in the home key of C, 2mz – this might equally represent the chord D F A C ... or the scale D E F G A B C D, depending on whether it is being used to indicate the harmony or the basis for melodic improvisation.
But must the scale always match the harmony? If one takes a simple song with no accidentals in its melody, it is clearly all being played in the one home key. Yet the harmony will be changing; it will typically progress through 1, 5z, 4x, 1, or through 1, 6myz, 2mz, 5z, 1. Clearly, a sequence of several harmonies is here being constructed on exactly the same set of notes. The bass note is changing, the subset of notes used to harmonise the melody is changing, yet these notes are all taken from the one scale.
A keyboard player, guitarist or bassist will need to play these changes. But a melodic improviser on any single-note instrument will not necessarily do so.
So we can distinguish between two types of harmonic changes in a song: static and dynamic.
Static changes, such as 1, 2mz, 5z, 1, are variations within the same home key. The bass note carries the sense of tonic from one place to another, but the chords being played all use selections of notes from the home scale. A melodic improviser can follow this by emphasising notes and patterns that express the chords, but he or she does not necessarily have to do so.
Dynamic changes, such as 1, y, 1, 3mz (the first 8 bars of “Out Of Nowhere”), actually involve changes of key in the melody, bringing in notes which are not in the original home scale. It is these that the melodic improviser must respect, since they involve changing the scale by bringing in accidentals.
Printed sheet music shows all the changes, typically one or two to a bar, but sometimes as many as three or four to a bar. The saxophonist, flutist, trumpeter etc. may discard most of these – certainly early in the learning process, and later on through choice. He or she has to analyse the song to extract the changes that matter – the dynamic changes – because it is on these scales that his or her solo must be constructed.
As one progresses, of course, one can return to a familiar song and find more harmonic detail in it which can be expressed in a solo.
Conversely, it seems that one can become more adventurous in finding scales which sound good over a given harmony, yet contain notes that don’t correspond to any simple major or minor scale. (For me, however, that’s a project for the future.)